
In my case Mersenne Twister is faster than the compiler’s built in pseudo random generator so there is no downside to using it.ģ. Originally I added Mersenne Twister after seeing it mentioned on this page by Inigo Quilez. I have seen some people say that Mersenne Twister is not required for Buddhabrots. A good (and fast) generator I use is the Mersenne Twister. For the Buddhabrot you need a random number function that can return a huge number of random values before they start repeating. The default random number generators in most compilers have a fairly low period of values before they start repeating the same numbers again. When looking for a random starting point for each orbit, the main cardioid and smaller 2nd period bulb areas of the Mandelbrot set can be easily detected and instantly skipped (saving the time of waiting for the z=z^2+c iterations to reach the maximum iteration value).įunction SkipCardioidAndCircle(a,b:double):boolean Ģ. Here are a few I found and implemented in the latest version of Visions Of Chaos.ġ. The above method will work and if you have a lot of patience you will slowly start to see a Buddhabrot image appear, but there are many ways to speed up the process of rendering Buddhabrots.

Goto 1 as long as it takes until a smooth image is rendered.

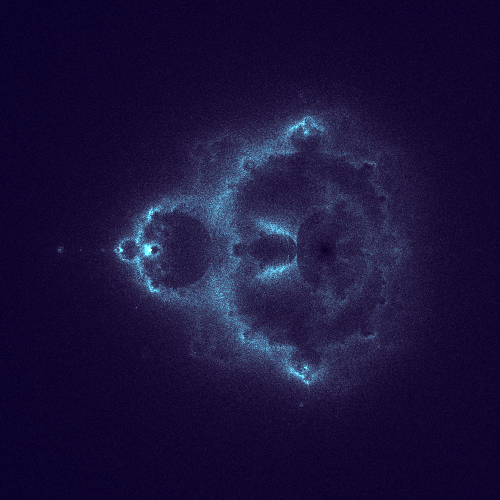
Every so often use the hitcount buffer to build the image you plot to the screen.ĥ. If z did exceed the bailout, it is a point not in the set, so reiterate the initial random point and each pixel it hits on screen you increase the hit count.Ĥ. Iterate z=z^2+c in the usual Mandelbrot way until the iterations reach a specified maximum iterations limit or the magintude of z is greater than a bailout value.ģ. A good range is between -0.5 and +2 for the real axis and -1.3 to +1.3 on the imaginary axis.Ģ. Pick a random starting point for complex C. These pixel hits accumulate and create the Buddhabrot image.ġ. To create a Buddhabrot image, you track the orbits of random starting points on the complex plane that are outside the Mandelbrot Set and count the number of times each on screen pixel is hit. This unique discovery led to the Buddhabrot images. Images based on orbit density plots had been explored before (see these examples from Linas Vepstas), but the Buddhabrot method was the first to ignore orbits that start within the Mandelbrot Set and only plot points outside the set. Just another case of Pareidolia if you ask me. The Buddhabrot was discovered by Melinda Green and named Buddhabrot because if you rotate the image 90 degrees clockwise it apparently resembles a sitting Buddha. They fall into the general catagory of an “orbit density” plot. Buddhabrots are a different way of visualizing the Mandelbrot Set.


 0 kommentar(er)
0 kommentar(er)
